【深度学习】注意力机制详细流程

自注意力机制

• 计算公式
  
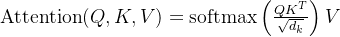
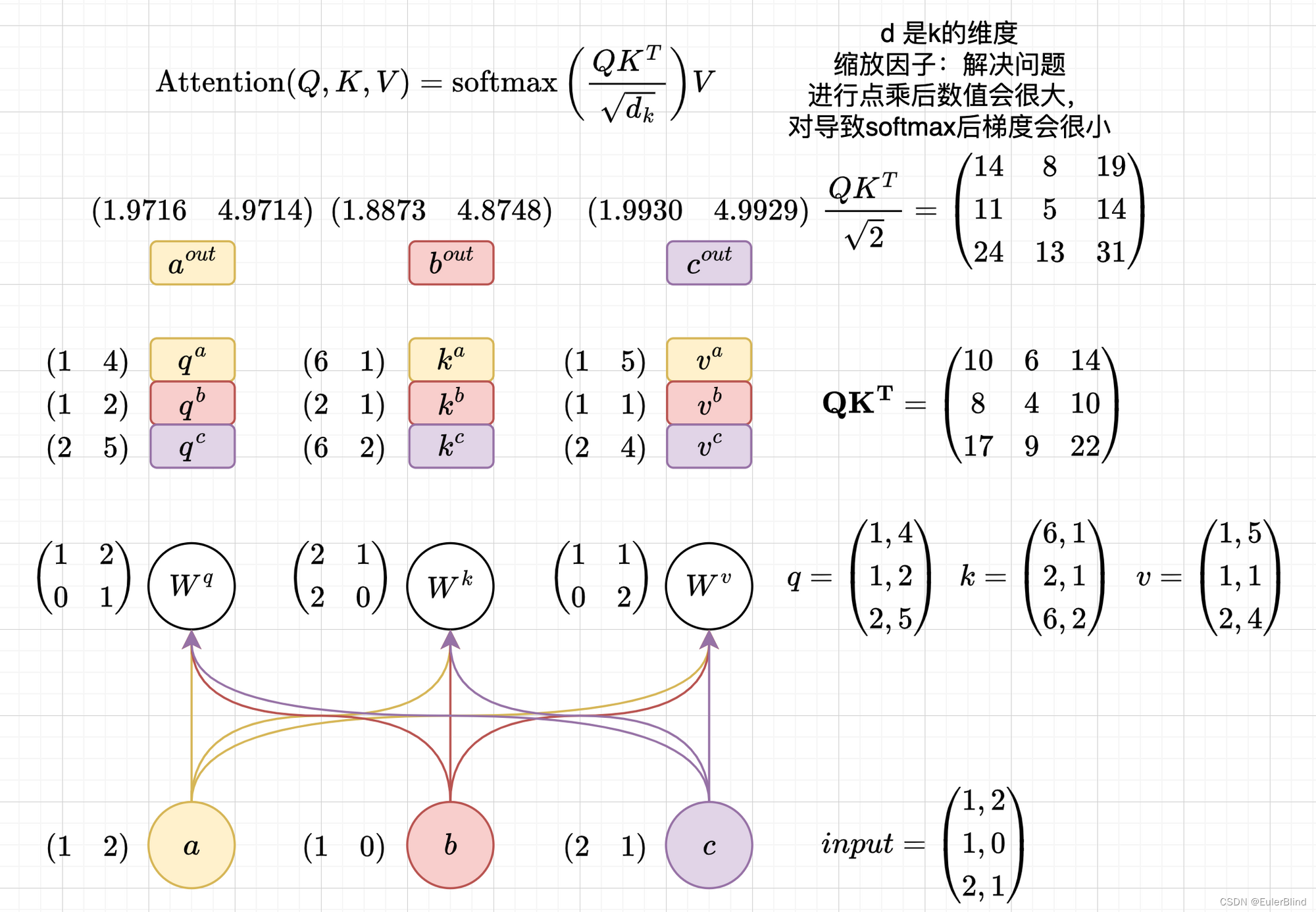
• 计算流程

编辑

• 相关代码

  import torch
  
  a = torch.tensor([1, 2], dtype=torch.float)
  b = torch.tensor([1, 0], dtype=torch.float)
  c = torch.tensor([2, 1], dtype=torch.float)
  # input
  input_tensor = torch.stack((a, b, c), dim=0)
  
  w_q = torch.tensor([[1, 2], [0, 1]], dtype=torch.float)
  w_k = torch.tensor([[2, 1], [2, 0]], dtype=torch.float)
  w_v = torch.tensor([[1, 1], [0, 2]], dtype=torch.float)
  
  q = torch.matmul(input_tensor, w_q)
  k = torch.matmul(input_tensor, w_q)
  v = torch.matmul(input_tensor, w_q)
  
  # 自注意力公式
  # $$
  # \\operatorname{Attention}(Q, K, V)=\\operatorname{softmax}\\left(\\frac{Q K^T}{\\sqrt{d_k}}\\right) V
  # $$
  # output
  output_tensor = torch.softmax((q @ k.T) / 2 ** 0.5, dim=1) @ v
  print(output_tensor)
  

  

多头自注意力机制

• 计算流程
  下图中为三个输入，分成两个head的情况，第一步根$W^q$,$W^k$,$W^v$求$q$、$k$、$v$跟自注意力机制中一致，不同处在于对于求取的$q$、$k$、$v$三个矩阵需要按照head个数 均分后再 组合，得到其中一个head结果$head_1^q$、$head_1^k$、$head_1^v$，在该head内部使用自注意力公式计算结果，由于这里给定的输入向量长度比较特殊，是一个1*2的向量，在head内部根据自注意力公式，softmax部分直接为1，其输出就是$head_1^v$。
  最后，根据划分的head个数，将每个head输出的结果进行组合，得到每个输入对应的输出结果。
  归纳一下，其计算步骤分为步。

  1. 根据$W^q$,$W^k$,$W^v$三个矩阵分别计算出$q$、$k$、$v$。
  2. 根据head个数对$q$、$k$、$v$进行均分操作。这里其实就算不能完全均分也是可以计算的。
  3. 将刚刚均分的结果以head为单位进行重新组合。
  4. 在每个head内使用自注意力公式，计算出每个head的结果。
  5. 根据head个数，将每个head计算结果进行重新组合，得倒每个输入对应的输出。

  编辑